Introduction
Optical pulse shapers that can modify the spectral phase and amplitude of an optical signal play a crucial role in various applications such as optical arbitrary waveform generation [1] and spectral quantum information processing [2]. Photonic integrated circuits (PICs) provide excellent platforms for pulse shaping, offering the advantages of compact size and potential for finer spectral resolution compared to commercial counterparts utilizing bulk optics.
One approach to on-chip pulse shaping is the use of arrayed waveguide gratings (AWG) [3, 4]. However, AWGs have drawbacks like fixed channel spacing, large footprint, and challenges achieving fine spectral resolution on the order of GHz. Microring resonators functioning as spectral filters could alleviate these problems [5], enabling a fine spectral resolution limited by the resonance linewidth and center frequency tunability via the thermo-optic (TO) effect. However, the large-scale control of these shapers becomes complicated by thermal crosstalk effects, and a truly programmable solution has not yet been shown.
This tutorial describes a method for programming microresonator-based integrated photonic spectral pulse shapers onto arbitrary frequency grids and with arbitrary phases. The method employs a simultaneous multi-heterodyne (MH) and dual-comb spectroscopy (DCS) measurement to control the channel position and phase, respectively. The technique is demonstrated by compressing lines from a 3 GHz electro-optic (EO) comb into transform-limited pulses in the time domain.
Experimental Setup
The pulse shaper PIC used in this work is built on the silicon-on-insulator (SOI) platform fabricated by AIM Photonics. The shaper has a single input waveguide coupled to an array of microresonators, as shown in Figure 1(a). Each resonator downloads a unique slice of the input spectrum and routes it to a TO phase shifter before being uploaded to a common output waveguide via an identical resonator.
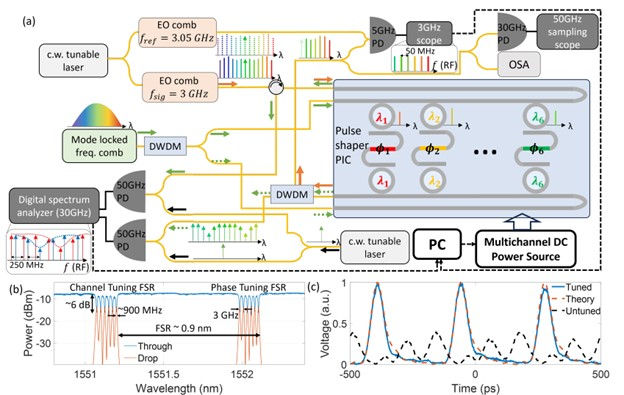
The resonators have a linewidth of 1.1 GHz, drop-port loss of 2.5 dB, and free spectral range (FSR) of 110 GHz. When combined to form a shaper channel, the linewidth is ∼ 900 MHz with ∼ 6 dB of insertion loss, as indicated in Figure 1(b).
Aligning Resonators and Tuning Phases
To align resonators within a shaper channel, a MH measurement technique with electronic feedback is implemented. A portion of the spectrum from a mode-locked frequency comb is sent through loopbacks on both the download and upload sides of the shaper. The strong coupling between the bus waveguides and resonators leads to a significant (∼ 10 dB) frequency-dependent extinction as measured from the output of the loopbacks, indicating the resonance frequencies of the resonators.
By combining the modulated comb exiting the loopback waveguides with a continuous wave (CW) laser emitting at a fixed wavelength and beating on a high-speed photodetector (PD), the optical response can be downconverted to the radio frequency (RF) range after measurement by an oscilloscope and fast-Fourier transform (FFT). This MH measurement enables multiple optical spectra to be measured simultaneously and supports high rates of spectrum measurement.
To measure the spectral phase applied to each channel, a DCS method with two EO combs generated using the same pump is adopted. The signal comb is driven with a frequency equal to the spacing of the shaper channels (fsig), and the reference comb is driven at a slightly different frequency (fref = fsig + Δf). The signal comb modes on the high-wavelength side of the pump are sent through the shaper to accumulate the phase applied by each channel.
The signal comb exiting the chip through the drop port is combined with the reference comb and sent to a balanced PD. Heterodyne beats at harmonics of the dual-comb difference frequency (Δf) are generated. The phase difference between the signal and reference comb can be measured by acquiring the generated electronic signal using an oscilloscope and sampling the phase at beat notes frequencies after an FFT.
The MH and DCS methods can be performed simultaneously by using the loopback waveguides bi-directionally and employing DWDM spectral filters, as shown in Figure 1(a). A Python-based control routine is implemented using these techniques to program the system to operate on uniformly spaced frequency grids and with arbitrary phases.
Pulse Compression Demonstration
As a first demonstration, the control routine is run to align shaper channels to a 3 GHz grid and compress six lines from the 3 GHz signal EO comb. The signal comb coming out of the chip is split by a fiber coupler. Half of the light is sent for DCS measurement, and the majority of the other half goes to a 30 GHz PD for time-resolved measurement of the waveform with a sampling oscilloscope.
To compress the lines from the signal comb, the routine is used to set the phase tuners such that the DCS measured phases are the negative of the reference comb spectral phase, which is measured to be approximately quadratic at ∼0.009 rad/GHz^2.
The initial temporal waveform, where the phase shifters in each channel are not yet tuned, is shown in Figure 1(c) (black dashed line). After running the control routine, the waveform is shown in Figure 1(c) (blue solid line), which agrees well with the theoretical prediction of a transform-limited pulse as measured through the system (orange dashed line).
The shaper transmission for the pulsed state as measured from a swept laser is shown in Figure 1(b). The entire control sequence takes just a few minutes to converge.
Conclusion
This tutorial described a method for programming microresonator-based integrated photonic spectral pulse shapers onto arbitrary frequency grids and with arbitrary phases. The technique employs a simultaneous multi-heterodyne (MH) and dual-comb spectroscopy (DCS) measurement to control the channel position and phase, respectively. The method was implemented experimentally on a 6-channel silicon photonic device with narrow linewidth resonators to compress lines from a 3 GHz electro-optic comb, demonstrating the potential of programmable pulse shaping for various applications in optical signal processing and quantum information science.
References
[1] S. T. Cundiff, A. M. Weiner. "Optical Arbitrary Waveform Generation," Nature Photon., vol. 4, pp. 760–766, 2010.
[2] H.-H. Lu, A. M. Weiner, P. Lougovski and J. M. Lukens, "Quantum Information Processing With Frequency-Comb Qudits," IEEE Photonics Technol. Lett., vol. 31, no. 23, pp. 1858-1861, Dec.1, 2019
[3] A. J. Metcalf, et al. "Integrated line-by-line optical pulse shaper for high-fidelity and rapidly reconfigurable RF-filtering," Opt. Express, vol. 24, no. 21, pp. 23925–23940, Oct. 2016.
[4] M. Gehl, et al. "Active phase correction of high resolution silicon photonic arrayed waveguide gratings," Opt. Express, vol. 25, no. 6, pp. 6320-6334, Mar. 2017.
[5] J. Wang, et al. "Reconfigurable Radio-Frequency Arbitrary Waveforms Synthesized in a Silicon Photonic Chip," Nature Commun., vol. 6, p. 5957, Jan. 2015.

Comentários