Biomedical Optics Express|The Wavelength Dependence of Blood Flow Index Revealed by Interferometric Near-Infrared Spectroscopy

Introduction

The quantification of blood flow in biological tissues is crucial for understanding physiological processes and diagnosing various medical conditions. One widely used optical technique for assessing tissue perfusion is Diffuse Correlation Spectroscopy (DCS), which measures the blood flow index (BFI) – an optically accessible parameter that serves as a proxy for tissue perfusion. BFI is defined as the product of the dynamic scattering probability (α) and an effective red blood cell (RBC) Brownian diffusion coefficient (DB).

Traditionally, DCS measurements have been performed in the near-infrared wavelength range, typically between 767-855 nm. However, the underlying assumption has been that BFI is wavelength-independent. This assumption has been rarely questioned, despite the potential for wavelength-dependent α to introduce inconsistencies in BFI measurements.

In this tutorial, we will explore a recent study that challenges the commonly held belief of wavelength-independent BFI. Using a dual-wavelength interferometric near-infrared spectroscopy (iNIRS) system, the researchers reveal that the dynamic scattering probability (α) and, consequently, the blood flow index (BFI) are indeed wavelength-dependent. We will also discuss the importance of incorporating higher-order mean squared displacement (MSD) cumulants in accurately modeling the field autocorrelation functions obtained from iNIRS measurements.

Dual-Wavelength iNIRS Setup

The key to this study's success was the development of a dual-wavelength iNIRS system, which allowed for simultaneous autocorrelation measurements at 773 nm and 855 nm (Figure 1). The system was designed to ensure that both wavelengths illuminated and collected light from the same spot on the tissue, minimizing any potential differences in the probed tissue regions.

Figure 1. Dual wavelength iNIRS setup. All fibers are single mode with angle polished connectors. I/C controller: current controller; DFB: distributed feedback laser; L,L’: lenses; APP: anamorphic prism pair; WDM: wavelength division multiplexer; DBD: dual balanced detector. Bold lines denote optical paths, while dotted lines denote electrical paths. Path 1 (red) is for 855 nm, while path 2 (blue) is for 773 nm.

The system employed two distributed feedback (DFB) lasers, one operating at 773 nm and the other at 855 nm. The lasers were sinusoidally modulated to achieve time-of-flight (TOF) resolution, with the modulation input voltages from a common function generator. This synchronized the wavelength tuning, ensuring that both wavelengths had matched TOF resolution.

The light from the two wavelengths was combined and delivered to the sample using a custom wavelength-division multiplexer (WDM). The remitted light was then separated by another WDM and recombined with the appropriate reference arm light before detection by dual-balanced detectors. This approach ensured that both wavelengths illuminated and collected light from the same spot on the tissue, a crucial requirement for meaningful comparisons of the autocorrelation functions.

Wavelength Dependence of Dynamic Scattering Probability (α)

The researchers investigated the wavelength dependence of α by applying two scaling methods to estimate the 773 nm autocorrelations from the 855 nm autocorrelations:

1. Constant α-scaling approach: This approach assumes that α is wavelength-independent, i.e., μ's,dyn = αμ's.

2. Constant μ's,dyn-scaling approach: This approach assumes that the dynamic scattering coefficient (μ's,dyn) is wavelength-independent, which implies that α is wavelength-dependent.

Figure 2: Ability to predict g^773_1(τ_s, τ_d) from g^855_1(τ_s, τ_d) by scaling the τ_d-axis for (a) Intralipid phantom and (b) human forearm. Note that 1-R^2 is shown, where R^2 is the coefficient of determination. The constant α-scaling approach performs best for the purely dynamic Intralipid phantom, whereas the constant μ's,dyn-scaling approach performs best in-vivo, with mixed static and dynamic scattering.

As shown in Figure 2, the constant α-scaling approach accurately predicted the 773 nm autocorrelations from the 855 nm autocorrelations in the Intralipid mixture, consistent with α = 1. However, in the in-vivo human forearm measurements, the constant μ's,dyn-scaling approach performed better, suggesting that α is indeed wavelength-dependent.

This wavelength dependence of α is further supported by the literature on RBC scattering, which indicates that the reduced scattering coefficient (μ's) of whole blood varies with wavelength, while the dynamic scattering (μ's,dyn) remains relatively constant (Figure 3). Consequently, the blood flow index (BFI = αDB) is also wavelength-dependent, as shown in Table 1.

Figure 3: (a) Spectral dependence of the scattering coefficient (μ_s) of whole blood from the literature. (b) Derived μ's = μ_s(1-g) of whole blood using the anisotropy factor (g) and μ_s. (c) Spectral dependence of tissue μ's with three different scattering powers. (d) Derived probability of dynamic scattering, α, from (b)-(c), assuming a 5% blood volume fraction.

Table 1. BFI of Intralipid and in-vivo forearm with their ratio across wavelengths

Importance of Higher-Order MSD Cumulants

The study also highlighted the importance of incorporating higher-order mean squared displacement (MSD) cumulants in accurately modeling the field autocorrelation functions obtained from iNIRS measurements. The researchers found that the commonly used single exponential model of Diffuse Wave Spectroscopy (DWS) [Eq. (2)] adequately described the autocorrelation functions for the Intralipid phantom (g_dyn ≈ 0.6), but failed to capture the slowly decaying tails of the in-vivo autocorrelation functions (g_dyn ≈ 0.98).

Figure 4. Measured G1 and single exponential fit for Intralipid mixture at different τs (855 nm) (EARLY τs: 60 ps, MID τs: 330 ps and LATE τs: 500 ps). The IRF and corresponding TPSF are shown in the inset of Figure 4(a).

Figure 5. Same as above but for 773 nm. The IRF and corresponding TPSF are shown in the inset of Figure 5(a).

Figure 6. Measured G1, single exponential fit, and Eq. (1) fit for human forearm at different τs (855 nm) (EARLY τs: 60 ps, MID τs: 330 and LATE τs: 500 ps). The IRF and corresponding TPSF are shown in the inset of Figure 6(a).

Eq. (1) ：

Figure 7. Same as Figure 6 but for 773 nm. The IRF and corresponding TPSF are shown in the inset of Figure 7(a).

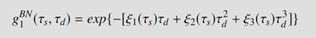
To better describe the in-vivo autocorrelation functions, the researchers employed a more comprehensive model [Eq. (1)] that incorporated higher-order MSD cumulants. This model was able to capture the slowly decaying tails of the autocorrelation functions, particularly at early and intermediate time-of-flights (Figures 18-20).

Eqs. (2), (3) and (4) ：

Figure 8. (a) Fitting g^773_1 at early τs of 60 ps with Eq. (13); (b) Predicting g^773_1 at early τs by scaling the recovered 855 nm ξ1(τs), ξ2(τs) and ξ3(τs) based on theory [Eqs. (2), (3) and (4)]; (c) Same as (b) but scaling each constant with (855/773)^2 ; and (d) Bland-Altman plot showing difference between fitting and measurement of (a), between theory-based prediction and measurement of (b), and between λ^2 scaling-based prediction and measurement of (c). (EARLY τs: 60 ps, MID τs: 330 ps and LATE τs: 500 ps)

Figure 9. Same as Figure 8 but for mid τs of 330 ps.

Figure 10. Same as above but for late τs of 500 ps. Differences in scaling approaches are less apparent due to low SNR.

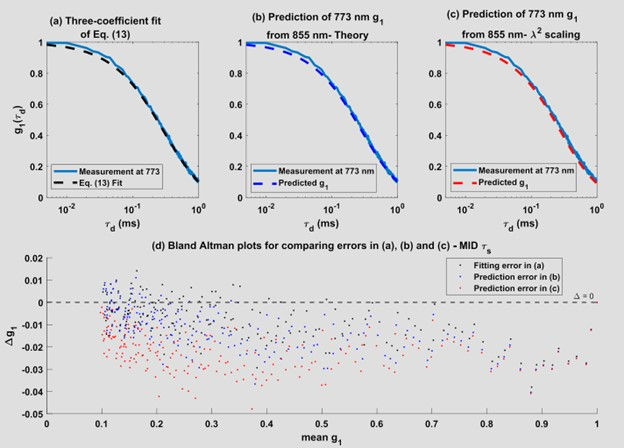
The researchers found that the higher-order MSD cumulant terms decreased with increasing wavelength, indicating that the tails of the autocorrelation functions are more pronounced at shorter wavelengths (773 nm) compared to longer wavelengths (855 nm). This observation aligns with the theoretical predictions and underscores the importance of considering higher-order MSD cumulants in accurate modeling of autocorrelation functions, particularly in applications such as laser speckle and DCS.

Conclusion

This tutorial has highlighted the key findings from a recent study that challenged the commonly held assumption of wavelength-independent blood flow index (BFI) in diffuse correlation spectroscopy. Using a dual-wavelength iNIRS system, the researchers demonstrated that the dynamic scattering probability (α) and, consequently, the BFI are indeed wavelength-dependent. This finding has important implications for the interpretation and comparison of BFI measurements obtained using different wavelengths.

Furthermore, the study emphasized the significance of incorporating higher-order mean squared displacement (MSD) cumulants in accurately modeling the field autocorrelation functions, particularly in biological tissues with high dynamic scattering anisotropy. This insight is crucial for improving the interpretation of laser speckle, DCS, and related modalities that rely on autocorrelation analysis.

The dual-wavelength iNIRS approach, along with the theoretical framework developed in this study, provides a robust methodology for investigating the wavelength dependence of optical parameters in biological tissues. These findings underscore the importance of careful consideration of wavelength-dependent effects in the interpretation of diffuse optics measurements, ultimately enhancing our understanding of tissue perfusion and other physiological processes.

Reference

[2] D. Mazumder, O. Kholiqov, and V. J. Srinivasan, "Interferometric near-infrared spectroscopy (iNIRS) reveals that blood flow index depends on wavelength," Biomedical Optics Express, vol. 15, no. 4, pp. 2152-2173, Apr. 2024. https://doi.org/10.1364/BOE.507373